طريقة التكرار بنقطة ثابتة
نقطة ثابتة
ليكن \(I\) مجال مغلق من \(\mathbb{R}\) و لتكن
\[\begin{split} g:I&\longrightarrow I\\ x&\longrightarrow g(x) \end{split}\]نسمي كل نقطة \(x^{*}\) تحقق
\[x^{*}=g(x^{*})\]بنقطة ثابتة ل \(g\) (لأن \(g\) تحافظ على \(x^{*}\))
التكرار بنقطة ثابتة
نحافظ على نفس الرموز، و لتكن \(\bar{x}\in I\)، نسمي المتتالية التالية
\begin{equation} \label{1} x_{n+1}=g(x_{n}),\, n\geq 0, \quad x_{0}=\bar{x} \end{equation}
بمتتالية التكرار بالنقطة الثابتة (Fixed Point Iteration )
نفرض أن الدالة \(g\) مستمرة، فنجد النظرية التالية
نظرية:
برهان:
بما أن \(\forall n, x_{n}\in I \)، و \(I\) مغلق، فإن
\[x^{*}=\lim_{n\to\infty}x_{n}\in I\]و بما أن \(g\) مستمرة فإن
\[\begin{split} x^{*}&= \lim_{n\to\infty}x_{n+1}=\lim_{n\to\infty} g(x_{n})\\ &=g(\lim_{n\to\infty} x_{n})\\ x^{*}&=g(x^{*}) \end{split}\]يمكن تطبيق هذه الطريقة لحل معادلات من الشكل
\[x=g(x)\]بشرط تقارب متتالية التكرار بنقطة ثابتة. نترك مسألة التقارب على جانب الأن، و نأخذ مثال
مثال تطبيقي
لنعتبر المعادلة
\[x=\cos(x)\]لكي نحل المعادلة في \(\mathbb{R}\)، يجب أن نكتب مسألتنا على الشكل الذي إعتبرناه، فهنا يمكننا إعتبار الدالة
\[\begin{split} g:[0,1]&\longrightarrow [0,1]\\ x&\longrightarrow g(x)=\cos(x) \end{split}\]و يمكن إختيار \(x_{0}=\bar{x}=0\)، و هكذا يمكننا صناعة متتالية من الشكل
\[\begin{cases} x_{n+1}=g(x_{n})=\cos(x_{n})\\ x_{0}=0 \end{cases}\]نستعمل نظام SageMath لحساب بعض الحدود لهذه المتتالية (إضغط على “Evaluate” لترى النتيجة)
يمكن أن نلاحظ (بدون برهان حتى الأن) أن المتتالية تتقارب
\[\lim_{n\to\infty}x_{n}=0.7390\cdots\]و هذا يعني (إذا كانت فرضية التقارب صحيحة) أن \(x^{*}=0.7390\) هو حل تقريبي للمعادلة
\[x=\cos(x)\]الشبكة العنكبوتية (Cobweb)
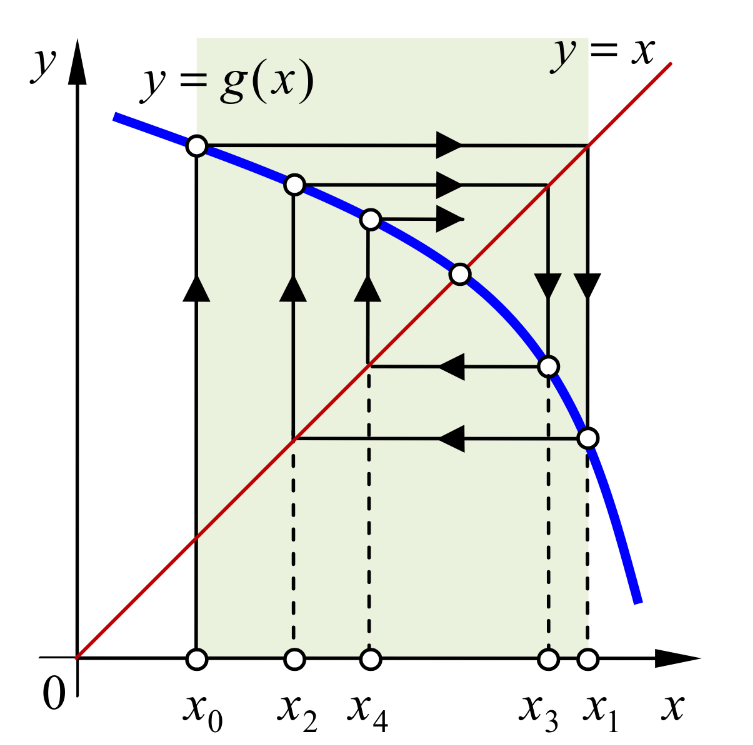
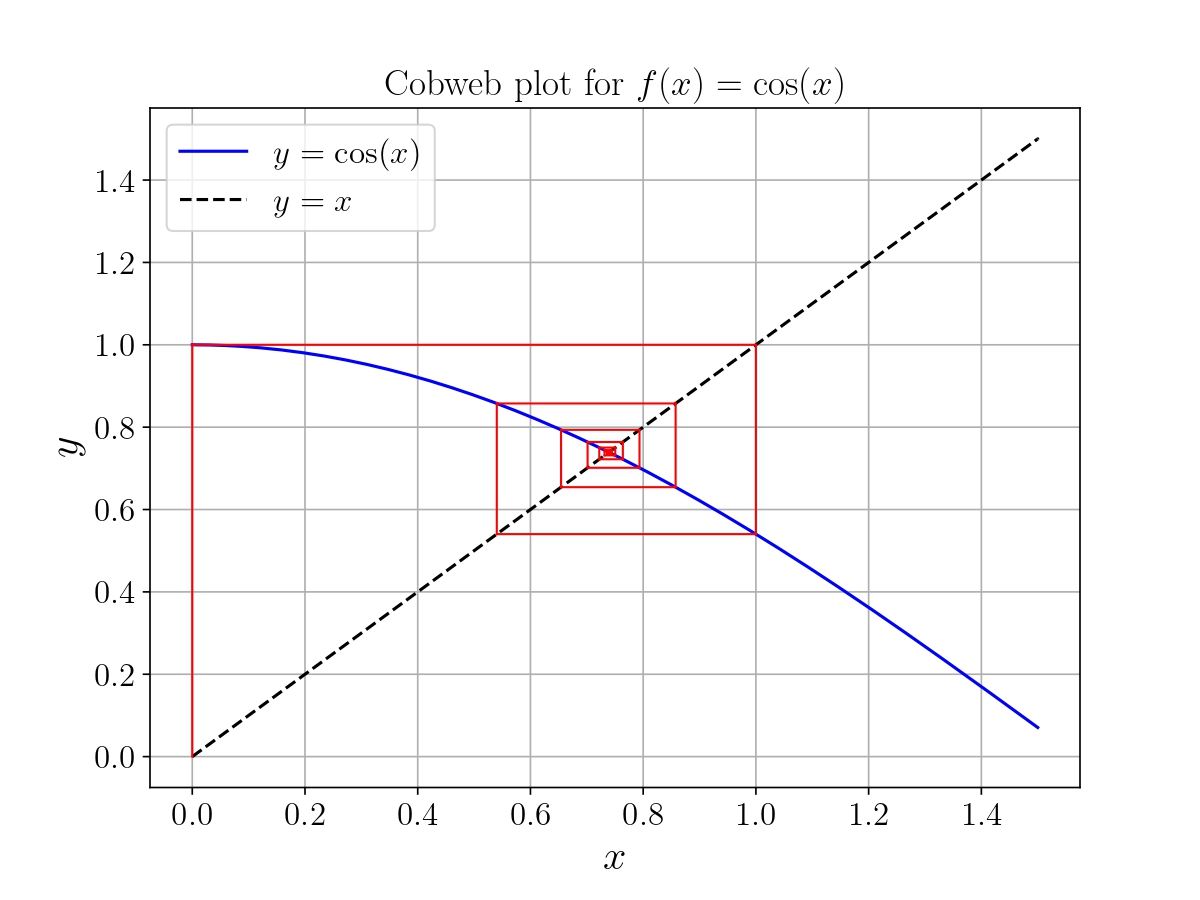
يمكن تمثيل عناصر هذه المتتالية بيانيا بما يسمى ب Cobweb (شبكة عنكبوتية، و ذلك لشكلها)، حيث نبدأ بحساب صورة \(x_{0}\) بإسقاطها عموديا على بيان الدالة \(g\)، فتعطينا \(x_{1}\). و لحساب \(x_{2}\) نريد جعل\(x_{1}\) سابقة، فنسقطها أفقيا على المستقيم \(y=x\)، ثم عموديا على بيان الدالة \(\cos\) فنحصل على \(x_{2}\)، و نكرر هذه العملية كما في الشكل السابق
نظرية باناخ للنقطة الثابتة
ليكن \(I\) مجال مغلق من \(\mathbb{R}\) و لتكن
\[\begin{split} g:I&\longrightarrow I\\ x&\longrightarrow g(x) \end{split}\]دالة مستمرة، و لنفرض وجود عدد حقيقي \(0<k<1 \) حيث
\[\forall x,y\in I, \quad |g(x)-g(y)|\leq k|x-y|\](الدالة \( g(\cdot)\) تسمى تقليص في هذه الحالة). هذا يعطينا النظرية التالية
